Het is weer lekker laat donker aan het worden! Dus langer licht. Ik had deze blogpost eigenlijk in het najaar willen schrijven, maar dat kwam er niet van. Toen vond ik het juist zo vroeg donker, en laat licht worden. Nu zul je iets zeggen van: Ja, dûh, het wordt altijd later donker in het voorjaar. (En in de winter ook trouwens, die begint zodra de dagen gaan lengen.) Dat klopt, maar het wordt wel sneller licht in het vroege voorjaar dan donker. En omgekeerd. In de late herfst is het weer anders: dan wordt het sneller later licht dan eerder donker.
Snap je het nog? Nee? Tijd voor een grafiekje, zo’n handig lijntje op millimeterpapier. Dat meer zegt dan duizend vergelijkingen. En daar moet je dan niet met een scheef oog naar kijken, maar met een recht oog, want de grafiek blijkt scheef te zijn.
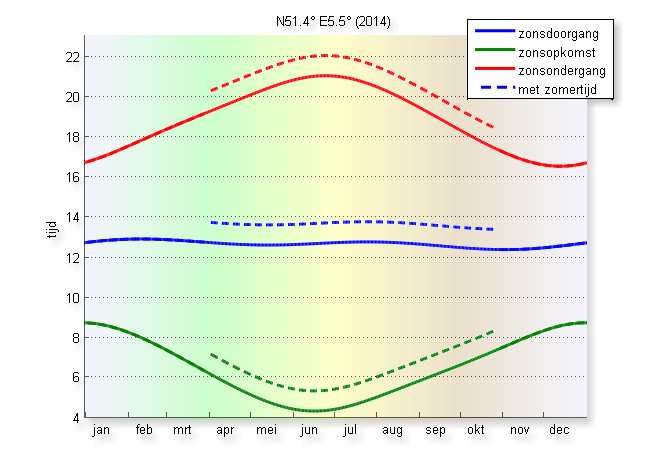
Duidelijk? Nee, niet helemaal. Want een grafiek zonder uitleg is als een kaart zonder legenda.
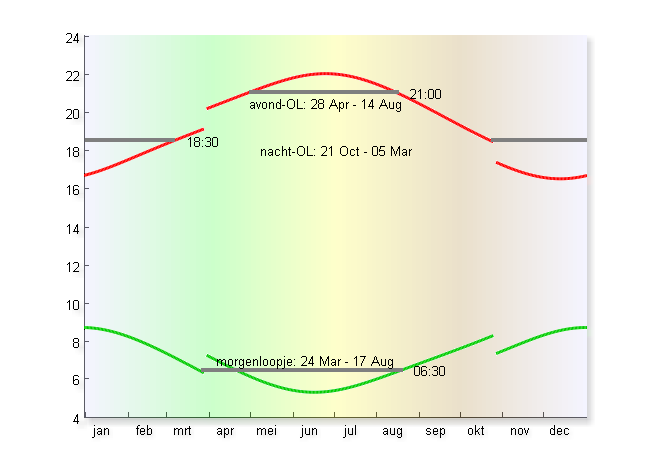
Je ziet de dag, zolang het licht is, tussen de de groene en de rode lijn. De aarde draait rondjes rond de zon, de aardas staat een beetje scheef (23,45°, lekker makkelijk te onthouden), en dus lijkt de zon door het jaar heen op en neer te slingeren aan de hemel (als je dagelijks op dezelfde tijd kijkt). Je zou in eerste instantie denken dat dat even snel op als neer zou zijn, mooi regelmatig. Maar het tijdstip van zonsop- en -ondergang is dat niet. De grafiek is scheef.
Heb ik deze gewoon fout getekend? Of berekend? Dat kan haast niet. Ik heb een beproefd algoritme gebruikt van een ouderwetse website in zwart-wit (gebruik deze als de andere link niet werkt), in mono gespatieerd lettertype. Dat moet wel kloppen. En een grafiek als hier boven kan je ook elders op internet vinden. Dat scheve, dat klopt gewoon.
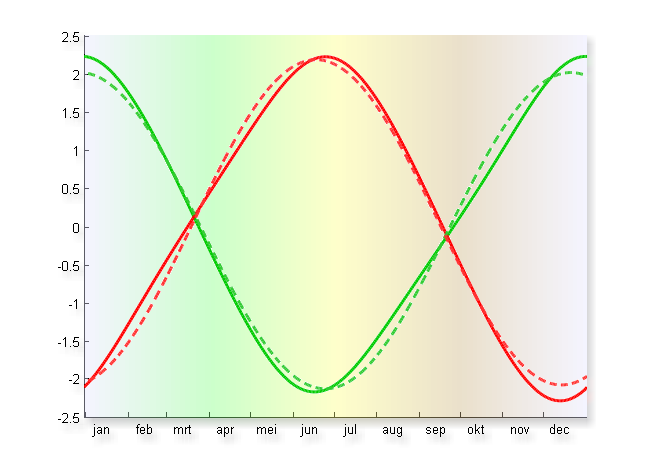
En dus ook de perceptie dat het zo snel donker wordt in de herfst. Zo veel dat het merkbaar is? Of vinden we het gewoon jammer dat het eerder donker wordt, en is het per definitie te snel? Laten we eens in meer detail kijken naar het verloop.
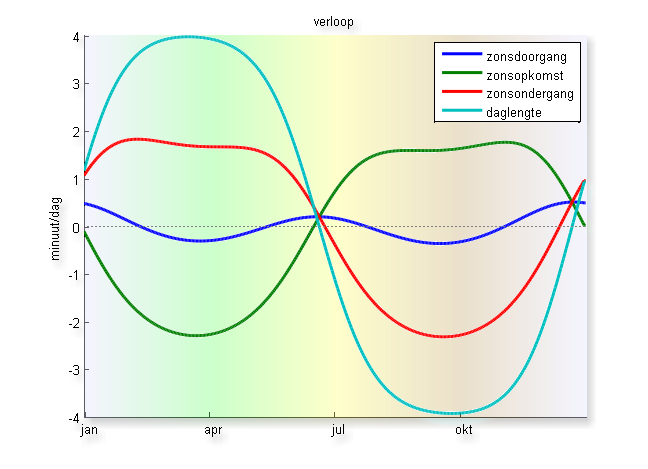
Hier boven zie je de afgeleide van de tijdstippen in de tijd, de verandering per dag. Dat maakt nog eens extra duidelijk hoeveel verschil er tussen de eerste en de tweede helft van het jaar bestaat: in de eerste helft verloopt de zonsondergang met hooguit 1’40” per dag, terwijl de zon tot wel 2’20” eerder opkomt per dag. En in de tweede helft is het precies omgekeerd. Maar die 1’40” per dag wordt wel vrij snel, in januari al, bereikt, en houdt aan tot begin juni, terwijl de 2’20” veel geleidelijker wordt bereikt, en even sloom weer afneemt.
Wat je ook ziet is dat het midden van de dag slingert, en misschien nog wel opvallender is het dat dat met een periode van een half jaar verloopt: twee keer per jaar verschuift het midden van achter naar voren en omgekeerd! Hoogst merkwaardig. En dan nog iets: het verloop van de daglengte, lijkt veel afgeplatter dan een normale sinusvorm. Terwijl de afgeleide van een sinusoide weer een sinusoide is. En dat is de daglengte dus niet. Zou het allemaal met elkaar te maken hebben?
En tenslotte kan je zien, als je goed kijkt, dat het snijpunt van de zonsopkomst- en -ondergang niet op de nullijn ligt (“0 minuten per dag”), maar er net boven, zowel op midzomer als op midwinter. Rond de kortste dag wordt het dus alweer later donker, maar ook nog stééds later licht. En na de langste dag blijft het nog even elke dag láter donker worden.
Ik zal nog een stapje verder gaan met mijn grafieken, en de afgeleide van de afgeleide berekenen, oftewel, de variatie in het verloop.
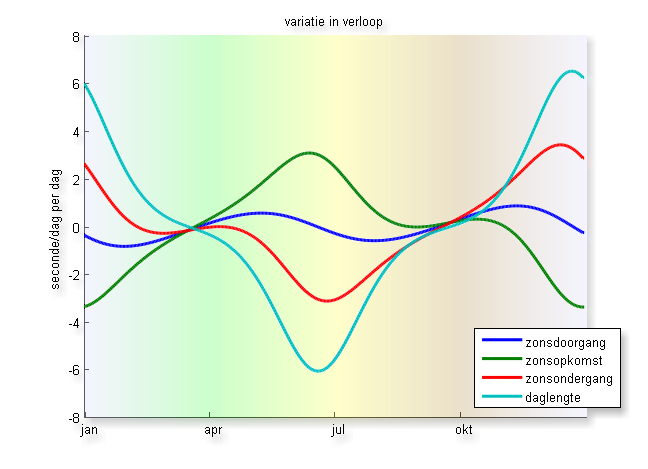
Eind winter, begin lente, zo zie je hier boven, lopen alle curves in de grafiek vrij vlak. Op de plek waar ze de nul-seconde-per-dag-per-dag lijn kruisen. Dus daar verandert de helling van het de zon-op/onder curve niet zo sterk: hij is daar afgeplat. Dat hadden we al eerder gezien. En in de herfst ook weer. Maar nu zie je dat dat niet alleen perceptie was, maar ook klopt. De daglengte-verandering verandert daar ook minimaal. Oftewel, een tijd lang wordt de dag dagelijks even veel langer, en een half jaar later korter. En bij de beide zonnewendes, midwinter en midzomer, verandert het juist heel scherp: ruim 6 seconden per dag per dag. Dus stel dat er twee dagen even lang zijn, dan is de daaropvolgende dag 6″ korter, die daarop 12″, die daarop 18″, etc. tot de daglengte bijna twee maanden lang met 4 minuten wordt verkort. En dát verloop, de daglengte, is in het voorjaar wél vergelijkbaar van vorm. Dus, hop, morgen heb ik weer vier minuten meer om bij daglicht te rennen.
Even een linkje leggen met oriëntatielopen: Nachtwedstrijden zijn er in de wintermaanden. Het moet vroeg genoeg donker worden zodat iedereen -eerlijkheidshalve- evenveel duisternis op zijn pad treft. De laatste nacht-loop is zo rond 5 maart (zon onder 18:15, start 19:00), en de eerste 25 oktober (zon onder 18:30, start 19:30). De zon moet dus minimaal een uur onder zijn. De (woensdag) avondlopen beginnen daarentegen weer half mei, als de zon zo rond 21:15 onder gaat, en starten tot 20:30. De laatste daarvan is zo eind augustus, als de zon om 20:45 onder gaat, en starten kan tot 20:00. Met andere woorden: voor een goede nacht-O moet het al een krap uur donker zijn, maar er wordt aangenomen dat er nog zonder hoofdlamp te lopen valt tot rond zonsondergang. En dan hangt de laatste starttijd af van de lengte van de route en dus de geschatte eindtijd. Nou ja, je kan natuurlijk ook twee uur eerder starten bij de zomeravondlopen, dus da’s een keuze.
Een volgende keer kom ik er op terug waardóór deze zonnetijden nu zo apert verlopen, en de plaatjes niet gewoon mooi symmetrisch zijn. Wil je op de hoogte blijven? Vul dan je email adres hier onder in, en je krijgt bericht als ik iets nieuws post.
Maar voor nu: onthoud gewoon dat we er ‘s avonds bijna het halve jaar lang ongeveer 1’40” bij krijgen. En dat het binnenkort maximaal snel vroeger licht wordt, maar dat dat even later weer vertraagt.
