Tijdens een rondje hardlopen schieten soms de vreemdste dingen te binnen. Dan ga ik ineens lopen rekenen, en kom tot de conclusie dat π zo gek nog niet is: τ hebben we in elk geval niet nodig, zoals in dit filmpje wordt gesuggereerd:
Ik liep een stuk (een forse taartpunt) tegen de klok in langs de Eindhovense ring, en bevond me in de buitenbocht. Ik kwam immers van buiten de ring, en was nog voor het oversteken rechtsaf geslagen, zodat ik op de ventweg linksom liep. De buitenbocht is om, dat weten we allemaal. Maar ja, het is wel een hele flauwe bocht, dus wat maakt het uit?
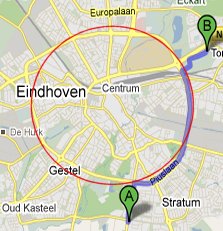
Ik volgde een tijdje de ring, sloeg toen af met het centrum in mijn rug, om later weer terug te keren op de ring. Dit maal liep ik met de klok mee, want ik ging weer richting huis.
Op een gegeven moment passeerde ik een tunnel, en besloot onder de ring door te gaan, om verder over de binnenbocht te lopen: veel korter, toch? Maar ja, al die tijd dat ik onder dat tunneltje door liep (of anderszins overstak van buiten naar binnen naar buiten in de bocht) was ik geen meter verder de ring rond gekomen.
Zo kwam het dat ik me afvroeg: hoeveel kilometer moet je over een rondweg lopen, wil het de moeite zijn om de binnenbocht te nemen? (Vooropgesteld dat je aan de buitenkant begint.)
Stel je voor: je gaat in de buitenbocht staan, loopt naar de binnenbocht, en direct weer terug naar de buitenbocht -omdat je helemaal niet de rondweg wilde volgen-. Dan is het overduidelijk dat het niet loont. Loop je echter het hele rondje, of twee, of oneindig veel keer, dan is het zeker wel de moeite van het oversteken waard. De waarheid ligt ergens in het midden. Maar waar?
Ik herinnerde me een vraagstuk van de middelbare school, waarop afgaande ik mijn vraag eigenlijk wat anders moest verwoorden: Stel, ik heb een touwtje rond de wereld gespannen, en dat wil ik een meter optillen. Dan moet ik het touwtje wel wat langer maken (gegeven dat het niet uit kan rekken). Maar als ik een touwtje rond een bal span, en de lus een meter ruimer maak -dus met overal een meter tussen bal en touwtje-, moet ik dan het touwtje meer of minder langer maken dan het touwtje rond onze aardbol?
Het antwoord is: geen van beide. Evenveel dus. 6,282 meter -en een beetje- om precies te zijn. Het klinkt ongelooflijk, dat een lus rond de hele aarde maar een ruime 6 meter langer hoeft te worden om 1 meter boven het aardoppervlak te zweven, en dat het niet uitmaakt of die planeet een straal van ruim 6300 kilometer heeft, of 15 centimeter, maar het is waar.
De lengte l van een cirkel met een straal r (de straal van de aarde of van de bal) is ![]() . Als ik het touwtje overal een meter boven het aardoppervlak houd wordt de lengte
. Als ik het touwtje overal een meter boven het aardoppervlak houd wordt de lengte ![]() , en als ik de lus een meter om de bal leg wordt zijn lengte
, en als ik de lus een meter om de bal leg wordt zijn lengte ![]() .
.
Maar dat kan ik weer schrijven als ![]() . En dus heb ik
. En dus heb ik ![]() extra touw nodig voor de bal, maar omdat
extra touw nodig voor de bal, maar omdat ![]() geld dat ook voor de aarde.
geld dat ook voor de aarde.
 Het maakt dus, volgens dezelfde redenering, niet uit of ik de rondweg rond een grote stad rond loop, of rond een kleine, maar het gaat om de hoek van de cirkelboog die ik volg. En dat is leuk, want dat betekent dat ik een vuistregel kan opstellen voor de beslissing of ik de ringweg oversteek of niet, afhankelijk van de grootte van de taartpunt (of het aantal graden dat ik de ringweg volg).
Het maakt dus, volgens dezelfde redenering, niet uit of ik de rondweg rond een grote stad rond loop, of rond een kleine, maar het gaat om de hoek van de cirkelboog die ik volg. En dat is leuk, want dat betekent dat ik een vuistregel kan opstellen voor de beslissing of ik de ringweg oversteek of niet, afhankelijk van de grootte van de taartpunt (of het aantal graden dat ik de ringweg volg).
Hoeveel graden moet je over een rondweg lopen, wil het de moeite zijn om -buiten beginnend- de binnenbocht te nemen?
Weet je wat? We gaan het gewoon uitrekenen! De vraag wordt nu: hoeveel graden moet je ronde een punt lopen, wil het de moeite zijn om de binnenbocht te nemen?
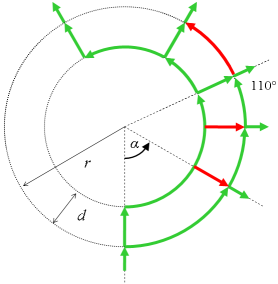 Laat de breedte van de rondweg d [meter] zijn, en de straal r. En je loopt vanaf 0° tot aan hoek α. Voor de berekening gebruiken we even
Laat de breedte van de rondweg d [meter] zijn, en de straal r. En je loopt vanaf 0° tot aan hoek α. Voor de berekening gebruiken we even ![]() , dus de hoek
, dus de hoek ![]() in radialen. De weg die je aflegt is dan
in radialen. De weg die je aflegt is dan ![]() via de binnenbocht, en
via de binnenbocht, en ![]() . Het loont dan dus als
. Het loont dan dus als ![]() , oftewel, als
, oftewel, als ![]() . Dat laat zich vereenvoudigen tot
. Dat laat zich vereenvoudigen tot ![]() , en dus
, en dus ![]() . Met andere woorden, als ik meer dan
. Met andere woorden, als ik meer dan ![]() rond ga, kan ik beter oversteken. Dat is dus bijna 115° (114,5915590261647…)! Best veel als je het zo bekijkt. Bijna vier uur op de klok.
rond ga, kan ik beter oversteken. Dat is dus bijna 115° (114,5915590261647…)! Best veel als je het zo bekijkt. Bijna vier uur op de klok.
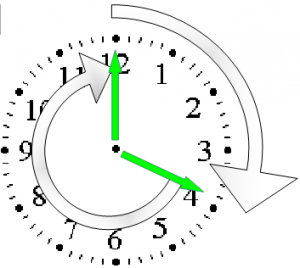 Onthoud dat goed: moet je meer dan één Pi-de deel van een taartpunt (een pie) rond een punt, neem dan voortaan de binnenbocht. En anders, ook al lijkt het om, kan je beter in de buitenbocht blijven.
Onthoud dat goed: moet je meer dan één Pi-de deel van een taartpunt (een pie) rond een punt, neem dan voortaan de binnenbocht. En anders, ook al lijkt het om, kan je beter in de buitenbocht blijven.
Het maakt niet uit hoe groot de cirkels zijn, zowel de binnenbocht, als de buitenbocht niet. 115° is 115°. Maar ik ben er wel van uit gegaan dat je alleen dwars (radieel) over kunt steken, dus niet spiraalvormig van buiten naar binnen en van binnen naar buiten of anderszins schuin, maar alleen in rechte lijnen van en naar het centrum.
Grappig vind ik het wel dat het antwoord niet ![]() e is of zo, maar
e is of zo, maar ![]() e. En dat is nou het leuke: eindelijk eens een redenering waaruit blijkt dat pi helemaal niet zo’n gek getal is. Anders had hier het
e. En dat is nou het leuke: eindelijk eens een redenering waaruit blijkt dat pi helemaal niet zo’n gek getal is. Anders had hier het ![]() -de deel van een cirkel gestaan, want
-de deel van een cirkel gestaan, want ![]() , en dan is een
, en dan is een ![]() -de toch veel mooier.
-de toch veel mooier.
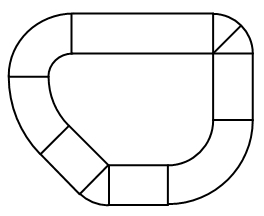 Je kan je trouwens nog even af gaan lopen vragen of het uitmaakt of de betreffende rondweg rond is, ei-vormig, onregelmatig, met rechte stukken er in, maar dat hoeft niet lang te duren want hier is het antwoord: Nee! Zo lang de binnen- en buitenbocht maar overal even ver uit elkaar liggen, en de weg overal convex is, gaat bovenstaande altijd op.
Je kan je trouwens nog even af gaan lopen vragen of het uitmaakt of de betreffende rondweg rond is, ei-vormig, onregelmatig, met rechte stukken er in, maar dat hoeft niet lang te duren want hier is het antwoord: Nee! Zo lang de binnen- en buitenbocht maar overal even ver uit elkaar liggen, en de weg overal convex is, gaat bovenstaande altijd op.
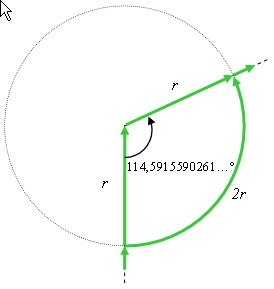
Je kan het zelfs nog eenvoudiger bekijken. Ga eens uit van een extreem brede rondweg, van de rand (straal is ![]() ) tot aan het midden van de cirkel (eigenlijk is de hele stad asfalt). Dan is de die weg
) tot aan het midden van de cirkel (eigenlijk is de hele stad asfalt). Dan is de die weg ![]() lang.
lang.
Een complete cirkel daarentegen heeft een omtrek van ![]() , en dus moet ik daar een
, en dus moet ik daar een ![]() e deel van hebben om op een cirkelboog van
e deel van hebben om op een cirkelboog van ![]() uit te komen, want
uit te komen, want ![]() .
.
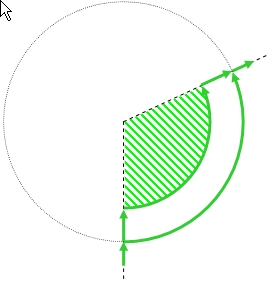 Geldt dat dan ook voor een weg van beperkte breedte? Ja! Want als ik bij deze specifieke hoek net zo goed om kan lopen als af kan snijden, kan ik ook evengoed en “hap” ter grootte van dit cirkelsegment uit een groter cirkelsegment nemen. En de resterende vorm is weer een stukje rondweg, met een even lange binnen- als buitenbocht. Q.E.D.
Geldt dat dan ook voor een weg van beperkte breedte? Ja! Want als ik bij deze specifieke hoek net zo goed om kan lopen als af kan snijden, kan ik ook evengoed en “hap” ter grootte van dit cirkelsegment uit een groter cirkelsegment nemen. En de resterende vorm is weer een stukje rondweg, met een even lange binnen- als buitenbocht. Q.E.D.