Category Archives: Overpeinzingen

It’s all about speed

14/09/2012English only, Overpeinzingen, WeglopenJan-Gerard

That’s great: at the bottom of this page, you can enter your own time and distance!

While running, I’m often wondering: while orienteering, it’s “which way?”, on the road, it’s “how fast?”. Like: “I am now running at a pace of 4’01”, I’m halfway my 1 km interval, how much fasther should I run to get to an average of 3’59” by the end of this interval, and how much does that differ on half a marathon?”. That type of questions.
[

Dutch version]

Some time ago, I discussed (and calculated!) that you shouldn’t be thinking while running, at least not when you already know whereto and how fast, but that is even more a motivation to do that beforehand. And, while running, dig the answers from your memory. That’s the reason for this article.

Let’s start simple: for once and for all -and that will be this year- I want to finish the Half Marathon within the one-and-a-half. So, that is 21.098 kilometer in 90 minutes. Dividing those figures results in a speed of 14.06 km/h (or 8.74 mph). With some experience I gained, I got a feeling for that speed. But still, it’s better to comprehend when express it as 234 meter per minute. And it sounds quite fast when I say 3.91 m/s (meter per second), which is about twice what I’m tall.

Since I take part in Orienteering races, the pace started to make sense to me (and because my GPS watch tells me). And now I know what it means to run 4’16”/km (4 minutes and 16 seconds per kilometer, or 6’52”/mile). The distance between two 'hectometerpaaltjes' (100 m signs)... I get a feeling for it. And, because I know that I have to keep that pace on the Half Marathon, it’s my reference for everything. 4’00” /km sounds already very quick, but recently, while training intervals with some colleagues, we incited each other easily to below 03’50” /km, and even with a sprint at the end, of 03’40” /km. Yet again, it’s easier to survey 100 meter than 1 km, especially when you want to estimate a distance on the road (the same as between the two ‘hectometerpaaltjes’). And, for my desired pace, I need to accomplish those 100 m within 25.60 seconds.

But what occupies me most, on my way, are the relative differences: how much faster should I run per 100 meter to finish one minute quicker? And, while running, I am typically not fit enough to realize that one minute contains about 60 seconds, so for each individual kilometer of the 21, that is let’s say 3. Or 0.3 seconds per 100 meter. That’s nothing! If that’s all for a finish time that’s one minute better, give me 10!

Below, a table, to observe the trends:

time	speed			pace		difference
hh:mm	km/h	m/min	m/s	min/km	s/hm	%	s/km	s/hm	pas/s	pas/min
01:20	15.82	264	4.39	00:03:47.54	22.75				1.45	87.02
01:25	14.89	248	4.14	00:04:01.76	24.18	1.18	2.84	0.28	1.36	81.90
01:26	14.72	245	4.09	00:04:04.61	24.46	1.17	2.84	0.28	1.35	80.95
01:27	14.55	242	4.04	00:04:07.45	24.75	1.16	2.84	0.28	1.33	80.02
01:28	14.38	240	4.00	00:04:10.30	25.03	1.14	2.84	0.28	1.32	79.11
01:29	14.22	237	3.95	00:04:13.14	25.31	1.13	2.84	0.28	1.30	78.22
01:30	14.06	234	3.91	00:04:15.98	25.60	1.12	2.84	0.28	1.29	77.35
01:31	13.91	232	3.86	00:04:18.83	25.88	1.10	2.84	0.28	1.27	76.50
01:32	13.76	229	3.82	00:04:21.67	26.17	1.09	2.84	0.28	1.26	75.67
01:33	13.61	227	3.78	00:04:24.52	26.45	1.08	2.84	0.28	1.25	74.85
01:34	13.46	224	3.74	00:04:27.36	26.74	1.07	2.84	0.28	1.23	74.06
01:35	13.32	222	3.70	00:04:30.21	27.02	1.06	2.84	0.28	1.22	73.28

You may have noticed that for every minute you subtract from your projected finish time, the required increase in speed, per minute, becomes larger. Not only the speed itself –that’s obvious– but the speed difference too. Meanwhile, the difference in pace is always the same. The relative difference, in %, of the time per 100 m changes, but the absolute difference, in s per 100 m, stays the same. It’s all logical, but it may be practical to remember while you’re on the go: time over distance (pace) is linear as a function of the finish-time; speed, and relative changes in pace, are inversely proportional.

When you run the first half 1″ per km slower than the 4’16”/km you should run, you will have to catch up those 21.098/2 s during the second half. To do that, you will have exactly half of the total 21098 m available. So you have to run exactly 1″ faster per km, than the overall average. The net difference is 2″/km with respect to you pace in the first half. Sounds easy.

For 1:30:00, you will have to run precisely 4’15.98”/km. Your GPS is not that accurate, but fortunately it’s close to 4’16”/km. However, you will just miss your target time by 19 ms. That is 19 milliseconds –not much, but all your hairs grow about one atom in that time, still at total of about 1/100 of a mm altogether. You miss your target by 7.1 cm! But, if you would have run 4’15”/km (the difference is hardly visible on your GPS watch), that will gain you advantage of 21 s at the end. Just a matter of approximation. Again, this a figure that is easily remembered: for every 1 second you run faster than planned, on a distance of 21.098 km, you gain in the end as many seconds as there are kilometers. For every distance!

If your run a a bit slower, and have to cache up at the end, then it may be interesting to express that lag in meters. Just as if, at that moment, you pick another runner -who keeps running at a constant pace- that many meters in front of yourself, and strive to overtake him right at the finish. Suppose, you ran 1 second to slow per kilometer. Then, at the end, you have to catch up that 21.098 s lag, what, right at the end (which is in fact too late) boils down to 82 meter. This way, it sounds quite tough. And, when you find out 1 km before the finish, that all the time you aimed at a pace 01:31:00, one minute too slow, then you have to overtake, in that last km, someone who, at that moment, is 223 meter in front of you. No, you’re not going to make that.

There are a few things to remember: Suppose you’re in terrific shape, and it goes very smooth. You can keep a pace of 4’00” /km, then you will finish at 01:24:23 Fantastic! To get a feeling for those finish times, I have written them on a dial: thinking in time like an old-fashioned clock is -for me at least- still the most intuitive representation. On top of the dial it says 4’00”, and ever second/km more counts clockwise. Can you print this one on your retina?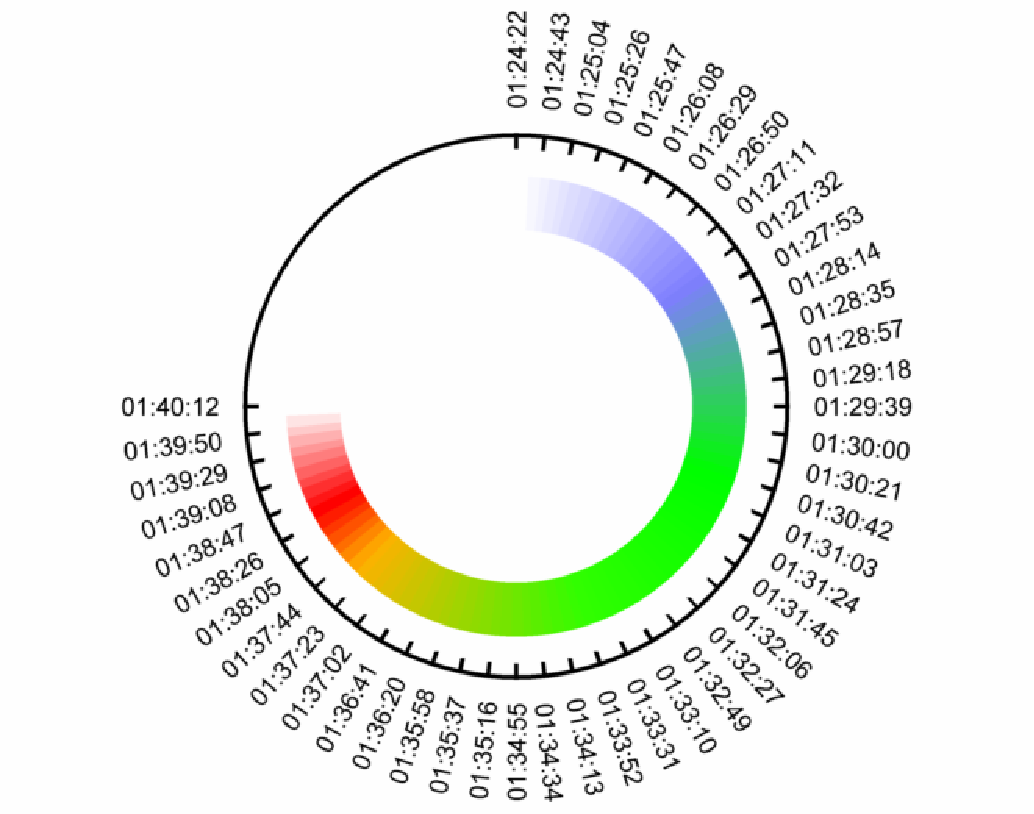

The moral of the story? Just run just below the 4’16” /km, and you need not think about anything. That saves a lot of energy!

Alles draait om snelheid

12/09/2012Overpeinzingen, WeglopenJan-Gerard

Da’s leuk: je kan onderaan deze pagina je eigen tijd en afstand invullen!

Tijdens het lopen loop ik vaak te denken. Bij het oriënteren vooral “waarheen?”, op de weg vooral “hoe snel?”. Zo van: “Ik loop nu 4’01”, ben halverwege mijn 1 km interval, hoeveel harder moet ik om 3’59” te lopen aan het eind van de kilometer, en hoeveel scheelt dat uiteindelijk op de halve marathon?”. Dat soort vragen. [

Enlish version]

Nou heb ik al eens uit lopen rekenen dat je eigenlijk helemaal niet moet denken tijdens het rennen, althans, niet als je al weet waar heen je moet en hoe snel, maar dat is des te meer reden om dat denken vooraf te doen, en onderweg de antwoorden uit je geheugen te putten. Vandaar dit verhaal.

Laten we simpel beginnen: ik wil ooit, en dat gaat dus dit jaar worden, de Halve onder de Anderhalf Uur lopen. Dat is dus 21.098 kilometer in 90 minuten. Op elkaar delen levert een snelheid op van 14.06 km/h. Met wat ervaring heb ik wel gevoel voor deze snelheid, maar het is toch beter te behappen als ik het uitdruk als 234 meter per minuut. En het klinkt best snel als ik er 3.91 m/s (meter per seconde) van maak, ongeveer twee keer mijn lichaamslengte.

Sinds ik oriënteer is ook het tempo me wat gaan zeggen (en omdat mijn GPS horloge het aangeeft), en weet ik ook raad met 4’16”/km (4 minuten en 16 seconden per kilometer). De afstand tussen twee hectometerpaaltjes... Maar dat is meer gevoel. En omdat ik weet dit tempo op de Halve te moeten gaan halen, relateer ik daar van alles aan. 4’00” /km voelt al behoorlijk rap, maar laatst intervallen gelopen met collega’s, en dan haas je elkaar snel tot onder de 03’50” /km, met een eindsprintje van 03’40” /km. Toch kan ik ook hier 100 meter weer beter overzien, ook om qua afstand in te schatten (dezelfde afstand als tussen twee hectometerpaaltjes), en bij het gewenste tempo moet ik die binnen 25.60 seconden afleggen.

Maar wat me vooral het meeste bezig houdt onderweg zijn de relatieve verschillen: hoeveel moet ik nu sneller lopen per 100 meter om een minuut eerder te finishen. En typisch ben ik onderweg niet scherp genoeg om te bedenken dat één minuut grofweg 60 seconden bevat, dus per enkele kilometer van de 21, pak hem beet 3 seconden, oftewel 0.3 s/hm. Dat is helemaal niets! Als dat alles is voor een één minuut snellere eindtijd, doe mij er dan maar 10!

Hier onder een tabelletje, om de trends te zien:

eindtijd	snelheid			tempo		verschil
hh:mm	km/h	m/min	m/s	min/km	s/hm	%	s/km	s/hm	pas/s	pas/min
01:20	15.82	264	4.39	00:03:47.54	22.75				1.45	87.02
01:25	14.89	248	4.14	00:04:01.76	24.18	1.18	2.84	0.28	1.36	81.90
01:26	14.72	245	4.09	00:04:04.61	24.46	1.17	2.84	0.28	1.35	80.95
01:27	14.55	242	4.04	00:04:07.45	24.75	1.16	2.84	0.28	1.33	80.02
01:28	14.38	240	4.00	00:04:10.30	25.03	1.14	2.84	0.28	1.32	79.11
01:29	14.22	237	3.95	00:04:13.14	25.31	1.13	2.84	0.28	1.30	78.22
01:30	14.06	234	3.91	00:04:15.98	25.60	1.12	2.84	0.28	1.29	77.35
01:31	13.91	232	3.86	00:04:18.83	25.88	1.10	2.84	0.28	1.27	76.50
01:32	13.76	229	3.82	00:04:21.67	26.17	1.09	2.84	0.28	1.26	75.67
01:33	13.61	227	3.78	00:04:24.52	26.45	1.08	2.84	0.28	1.25	74.85
01:34	13.46	224	3.74	00:04:27.36	26.74	1.07	2.84	0.28	1.23	74.06
01:35	13.32	222	3.70	00:04:30.21	27.02	1.06	2.84	0.28	1.22	73.28

Wat bijvoorbeeld opvalt is bij elke minuut dat ik sneller loop, de benodigde snelheidstoename, per minuut, steeds groter wordt. Maar het verschil tussen de tempo’s is steeds gelijk. Het relatieve verschil, in %, van de tijd per 100 m varieert, maar het absolute verschil, in s per 100 m, is telkens gelijk. Op zich logisch, maar handig te onthouden voor onderweg: tijd per afstand is lineair in de termen van de eindtijd; snelheid, en relatieve tempoverschillen, zijn omgekeerd evenredig.

Als ik de eerste helft 1” per km langzamer loop dan de 4’16”/km die ik zou moeten halen, moet ik in de tweede helft dus die 21.098/2 s inhalen. Daar heb ik in meters weer precies de helft van 21098 m voor tot mijn beschikking, dus moet ik per km precies 1” sneller lopen dan gemiddeld. Het netto verschil is dan 2”/km ten opzichte van het tempo op de eerste helft. Klinkt alsof dat met twee vingers in de neus moet lukken.

Voor de 1:30:00 moet ik precies 4’15.98”/km lopen. M’n GPS is niet zo nauwkeurig, maar gelukkig ligt dat vlak bij de 4’16”/km. Toch zou ik net mijn streeftijd missen met 19 ms. Op een haar na? Slechts 19 milliseconde –niet veel, maar in die tijd groeien al m’n haren ongeveer een atoomlengte, wat bij elkaar op iets van 1/100 mm haar neerkomt, 5 keer minder dan 1 haar dik is. Maar je raakt de finishlijn op 7.1 cm na! Als ik nou 4’15”/km zou lopen (het verschil is op mijn GPS horloge niet te zien) levert dat me op het eind ruim 21 s voorsprong op. Kwestie van afronden. Ook dit getal is weer heel eenvoudig te onthouden: als ik op 21.098 km elke km 1 s sneller loop dan gepland levert me dat op het eind evenveel seconden als kilometer op.

Loop ik nou wat langzamer, en moet ik dat gaan inhalen op het eind, dan is het interessant hoeveel dat is uitgedrukt in meters. Alsof ik op dat moment een loper op evenzoveel meter voor me kies -die constant tempo blijft lopen-, en ik die vervolgens in ga halen. Stel, ik loop per kilometer 1 seconde te langzaam. Dan moet ik op het eind die 21.098 s achterstand inhalen, wat, helemaal op het eind (eigenlijk is het dan dus al te laat) neer komt op 82 meter. Zo klinkt dan dan weer best pittig. En kom ik er 1 km voor de finish achter dat ik heb ingezet op een tempo dat neerkomt op 01:31:00, een minuut te lang, dan moet ik in die laatste ene km iemand inhalen die op dat moment ruim 223 meter voor me loopt. Nee, dat gaat niet meer lukken.

En dan zijn er nog een paar dingen handig te onthouden: Stel dat het nou heel lekker gaat, en ik precies 4’00” /km loop, kom ik op 01:24:23 op de hele afstand uit. Fantastisch! Om gevoel voor deze tijden te krijgen heb ik ze maar eens op een wijzerplaat getekend: denken in tijd als een ouderwetse klok is -voor mij althans- nog steeds het meest intuïtief. Bovenaan de wijzerplaat staat 4’00”, en elke seconde er bij telt rechtsom.

De moraal van dit verhaal? Loop gewoon net onder de 4’16” /km, en je hoeft nergens over na te denken.

Zo moet het dus! Lenteloop Complex Zuid

08/06/2012Overpeinzingen, Verbeterpuntjes, WedstrijdJan-Gerard

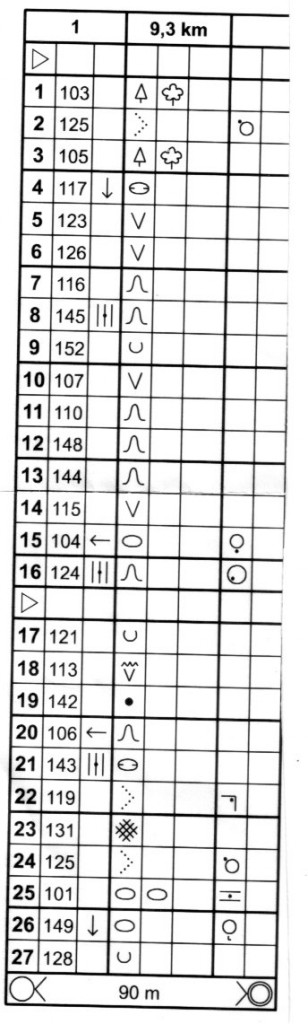
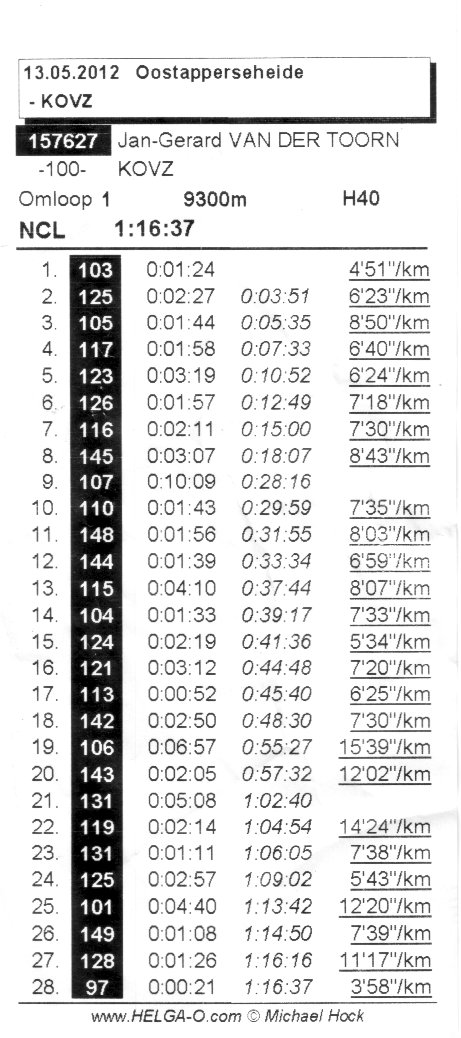
Wat ging dat lekker! Zie je trouwens rechts-boven een samenvatting van deze wedstrijd staan? Dat is nieuw. Heb ik alle relevante getallen en links naar kaart, video, splits en uitslagen in gezet. Alleen wil dit nog niet printen, maar daar vind ik wel wat op.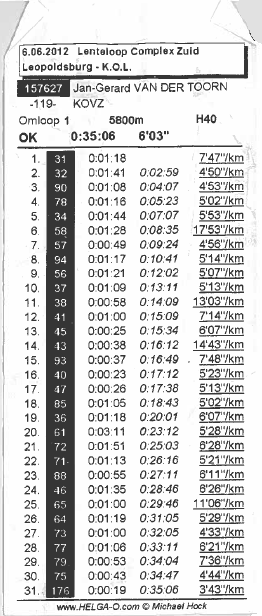

Terug naar de wedstrijd. Sowieso weer een mooi avontuur. Voor het eerst een sprint, korte afstandjes, veel posten, en in een “stedelijke” omgeving. Nou ja, stedelijk? We liepen over een schijnbaar verlaten militair kazerne-terrein. Tanks her en der, maar nergens mannetjes in groene pakken te zien. Door alle gebouwen en andere objecten was het echter uitstekend oriënteren. Soms was er geen kunst aan!

Gezellig meegereden naar de locatie, met 5 man in de auto. Dat verhoogt al de voorpret, en het is een stuk relaxed-er dan wanneer ik zelf, uiteraard net iets te laat, naar de start scheur. De hele auto zat zich al te verheugen.

Au! Een Sprint…

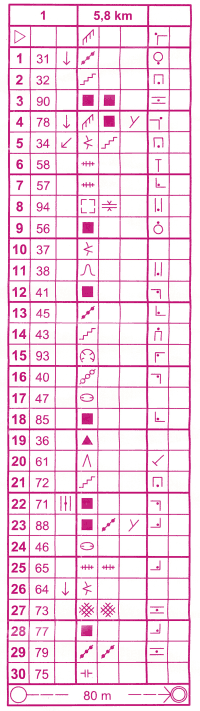De langste afstand was, in vogelvlucht, 5800 meter. Best kort, dus ik dacht er nog even over om twee omlopen te doen. Maar het bleek maar goed dat ik dat niet deed, want sprint is ook echt sprint, en bij de finish voelde ik dat ik alles gegeven had. Pittig! En leuk, om zo hard te gaan. Misschien let ik de volgende keer tevoren wel beter op als ik mijn tas inpak, en stop ik mijn weg-schoenen er in in plaats van mijn nieuwe Inov-8’s met stalen noppen. Want die maken zo’n herrie op straten en stoepen, waar het hier vol mee lag.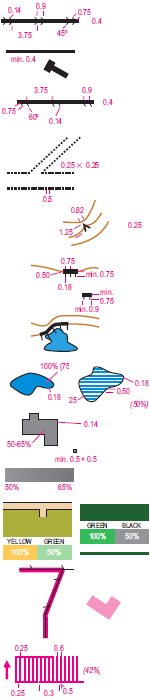

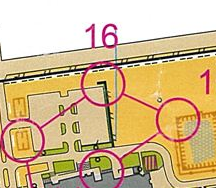Even had het er op geleken dat ik niet eens ging starten. Op weg naar de start-locatie namelijk, lette ik niet goed op, keek wat om me heen, verbaasde me dat mijn GPS-horloge maar 4 satellieten zag, en miste een laag hekje, waardoor ik voor ik het wist zijwaarts door de lucht vloog, hard op mijn heup landde, en een paar millimeter vlees van mijn elleboog bij wijze van kreukelzone op het asfalt achterbleef, verruild voor mos en modder in de wond. Au!

Tanden op elkaar, doorlopen naar de start, en niet zeuren. En warempel, zodra het piep-piep-piep-pieieieieieiep had geklonken van de start-timer, geen seconde meer aan gedacht. In elk geval geen 5, wat het verschil had gemaakt tussen een 7e en 8e plek.

Andere regels

Hier mag je niet overheen of doorheen. Herken je ze allemaal?

Het was dus een sprint. Achteraf hoorde ik dat dat betekent dat er ook andere regels gelden. Eentje daarvan is dat je hekjes, laag of hoog, die op de kaart staan niet over mag. Als je goed kijkt zie je dat er twee lijn-diktes worden gebruikt. Zou dat het verschil maken? Het is lastig al rennend het verschil in lijn-dikte te beoordelen. In dit geval stond er een post net over een laag hekje heen. Je kon er omlopen, dat scheelde 3 meter. Maar je kon er vanaf de andere kant ook heel makkelijk bij, zonder over het hekje heen te klimmen. Gewoon met de hand. Mag dat? Ik hoorde achteraf van niet. Hoeveel mensen zouden zijn omgelopen?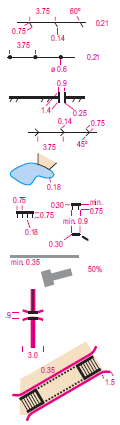

Ik vind het wel een gemene situatie, in dit geval. Als dit echt een punt van disqualificatie was, vind ik dat de baanlegger een overtreding hier ook wel uitlokte. De post zie je vanaf 100 meter al staan, je rent er recht naartoe, strekt je arm en legt de EMIT in, en rent verder. Dat de post over het hekje stond valt nauwelijks op. Wat vinden jullie?

Hier mag je wel passeren — En deze kenmerken mag je juist wel passeren. Soms lijken ze aardig op wat niet mag. Een hek met enkele dwarsstreepjes is dus toegestaan te passeren.

En zijn er nog meer van dit soort regels? Ja, je kan ze hier, op de IOF site, nalezen. Dikke lijnen (met of zonder dubbele dwarsstrepen): muren, railings, pijplijnen en kliffen die verbodenzijn. Meren met een zwarte lijn er omheen: ook verboden. Tunnels eveneens, tenzij anders aangegeven. En je mag ook niet over gebouwen heen.

Dan zie ik nog een speciale kleur donker-groen en groen-geel. Laat er eergisteren nou net bij post 11 zo’n dicht begroeide aarden wal gelegen hebben, waar iedereen overheen is gegaan, aan het spoor te oordelen. Allemaal gedisqualificeerd! Of lijkt het groen alleen maar donkerder dan dat van langzaam bos?

Ook interessant te lezen dat ‘controls may not be placed inside caves’. Ik moet ineens aan post 5, 10 en 26 van afgelopen donderdag denken, met het ‘cave’ symbool in de postomschrijving.

Nog beter?

Terug naar mijn resultaat. Ik heb zelden zo goed gelopen. Misschien ben ik gewoon goed als het om snelheid gaat, en niet om zoeken in natuurlijk terrein. Maar 8e van een veld van 60 deelnemers smaakt naar meer. In plaats van op mijn lauweren te rusten vraag ik mij af: Hoe doe ik het de volgende keer nog beter?

Bij post 5 maak ik ineens een gekke draai, nadat ik er aanvankelijk recht op af liep. Zag ik een andere loper? Nee, ineens een ondergrondse ingang. Dat zal hem wel zijn!? Kijk op de kaart, man! En vervolgens naar 6. Helemaal de kluts kwijt, loop ik recht op het heuveltje af, klim dwars door brandnetels een put in, ploeter er weer uit, en vind de post. Dat dan weer wel.

Ik liep 4″43′ langzamer dan de winnaar. Op de 35’06”. Dat is dus iets meer dan 10%. Maar dat is gemiddeld. Een paar posten springen er echt uit. Naar 6, 15, 19, 25 en 28 liepen de snellere lopers 25 tot 60% sneller dan ik. Waarschijnlijk vooral omdat ik daar liep te klooien op zoek naar de post.
Stel nou eens dat ik die net zo snel gevonden had als de rest. Dan had me dat 47″ + 7″ + 10″ + 20″ + 9″ = 93 seconde gescheeld. Anderhalve minuut. Daar win ik dus niet mee. Scheelde me 1 plaats, maar die had ik al gewonnen door 5 seconde sneller te lopen.

Dit is dan 19. Ik kom aan vanuit het westen. In een boogje naar de post. Maar daarna, wat doe ik dan? Slaat nergens op.

Had ik harder kunnen lopen? 5’17″/km is langzamer dan wat ik op de halve marathon haal: dat is 4’18″/km. Maar ja, dit is wel ander terrein, dus of dat ooit gaat lukken is de vraag. Toch geeft het aan dat er ruimte is voor verbetering.
In elk geval loopt de winnaar vrijwel overal sneller dan ik, en dat komt niet altijd door mijn zoek-talent. Dus ik moet ook zorgen dat ik harder ga. Het is per slot van rekening maar een paar km, zo’n sprint.

24 had ik wat slimmer kunnen aanlopen. Ik zie dat ik vooral veel snelheid verlies, omdat ik, in het bos nog, al denk dat ik er ben en ga zoeken. Op weg naar 25 vertel ik me ook: mijn passen zijn korter dan gedacht, en ik houd al te vroeg in. Bovendien zijn er wat "interessante" putjes in de grond, op plaatsen vergelijkbaar met waar ik eerder een post vond.

Het EMITten had ik dit keer aardig in de vingers. Tevoren post-nummer gecheckt en kaart gekeken voor vervolg, blijven kijken naar je hand bij inleggen, en EMIT oriënteren naar post vlak voor ik er was. Dus daar valt niet veel meer uit te halen.
Had ik kortere routes kunnen kiezen? Dat ik nog een leuke vraag. Laten we dat eens analyseren.

Kortste routes

Terwijl ik aan deze alinea begin heb ik hoge verwachtingen. Maar nu ik beter kijk valt het aantal benen dat een spannende routekeuze oplevert vies tegen. Ik kan er maar 4 vinden waar ik een beetje twijfel bij heb. We meten het even na:

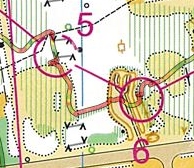
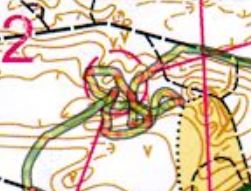
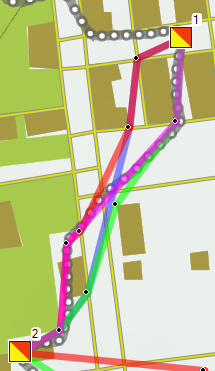Op weg van post 1 naar 2 kan je op vier manieren lopen. Groen is in het plaatje de kortste optie (371 m), blauw en magenta (mijn route), zijn even lang (381 m), en rood is met 384 m het langst. Maar het scheelt hooguit 13 meter. Wat is dat nou?

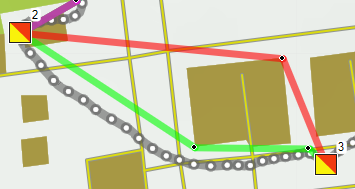Van 2 naar 3 zijn er ook twee mogelijkheden, maar hier is de groene met 245 m overduidelijk korter dan de rode route van 267 m.

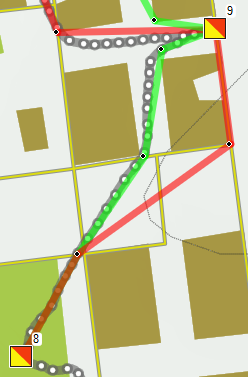Van 8 naar 9 kan je ook op meerdere manieren, maar het verschil lijkt duidelijker dan het is: 14 meter op een totaal van 282 m. Nou ja, dat is toch 5%, dus als je een paar procent wilt winnen is dit toch lonend. Bovendien kom je dan bij 9 op een gunstiger manier aanlopen, en zie je de post al staan, alhoewel dat tevoren nog niet zo duidelijk was.

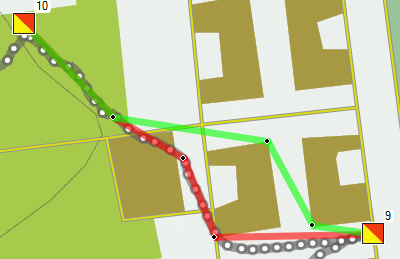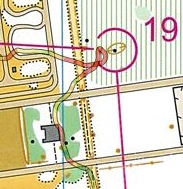
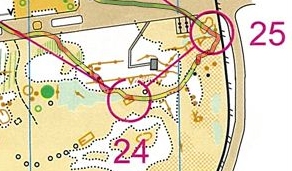
Op weg van 9 naar 10 viel 8 meter te winnen (of te verliezen, zoals ik deed). Maar ik denk dat dat op de echte kaart wel eens mee zou kunnen vallen, omdat de gebouwen wat breder zijn dan hier getekend. Alleen heb ik nog geen handig tooltje gevonden om op bitmaps te tekenen (ik kan ze wel als GoogleMap overlay in mijn browser krijgen) en om lengtes van lijnen/routes te bepalen (tekenen op een Google map gaat wel, maar dan weer niet op een Custom-overlay), dus heb ik hier Mapsource voor gebruikt.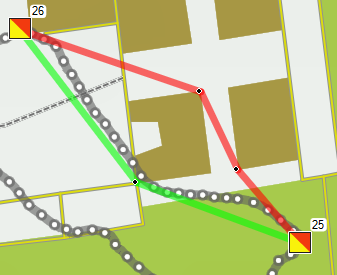

En tenslotte was er nog het been van 25 naar 26. Ook hier weer blijk ik de juiste keuze gemaakt te hebben, en heb de 5 meter kortere route gekozen. Poeh, wat knap! Op de 258 resp. 263 meter maakt dat nou niet ze heel veel uit.

Conclusie

Sprinten is leuk! En ik ben er best goed in. Door geen foutjes te maken kan ik 30% van het verschil verbeteren; ofwel 4% van mijn tijd. Misschien kan ik nog 5% harder gaan lopen, maar 10% zit er denk ik niet in; het is geen recht parcours over asfalt. En met mijn kortste-route inzicht hier boven valt er ook nog wel 0.2% te halen. Ik kom nog 1-2% te kort dan voor een 1e plaats. Wat een uitdaging!

Oriënteringslopen of Oriëntatielopen?

31/05/2012Overpeinzingen, Verhaal, WebsiteJan-Gerard

PlOts bOtste Ondergetekende Onlangs Onverwacht Op Onderstaande Overweging:

Is het Oriënteringslopen of Oriëntatielopen?

Ik dacht altijd het eerste, maar ik kwam een flyer tegen, ik denk van de NOLB, waarop in rood-witte sierletters Oriënteringslopen staat. Prompt heb ik de titel van mijn weblog aangepast. Toch zat het nog niet lekker. Ik heb deze vraag dus maar op het I-OL.nl forum gepost. Er ontstond meteen een discussie. Nu, een paar maanden later, is deze wel uitgedenderd.

Koen schrijft:

Nederland gebruikt oriënteringslopen, België oriëntatielopen. Zelf geef ik ook de voorkeur aan de tweede. […]

Oriëntering zie ik vooral bij Defensie, geen idee waar die verschillen ooit ontstaan zijn!

In het Engels is het duidelijk; daar heet het orienteering (wat ook makkelijker typt, zonder ümlaut). Maar ook in Zweden en Noorwegen heet het orientering, zij het met één “e”. Op zich klinkt het dan logisch als het Nederlandse woord in navolging daarvan “oriëntering” zou zijn.

Maar ja, een woord is een woord, en het kan vele oorsprongen hebben. (Zo zal het je verbazen -dat deed het mij althans- waar de uitdrukking “dat is toch baanleggerij van lik-me-vestje” vandaan komt.) Misschien moeten we het daar zoeken.

Clemens schrijft:

In de beginjaren van de NOLB heeft het oriëntatielopen geheten. Ik ben geen specialist maar als ik het me goed herinner is oriëntatielopen niet correct Nederlands en heeft iemand uit de beginjaren van de NOLB dit destijds gewijzigd. OL is afgeleid van het werkwoord oriënteren.

Dat geeft houvast. Er is maar één werkwoord oriënteren. Maar tegelijkertijd zijn er wel twee zelfstandig (of zijn het zelfstandige?) naamwoorden aan verbonden: oriëntatie en oriëntering. Dat maakt het lastig. En als je er dan weer een werkwoord van maakt door er -lopen achter te plakken, heb je dus twee mogelijkheden, oriënteringslopen en oriëntatielopen.

Als je de diverse online woordenboeken er op na sla (een mooi overzicht van diverse bronnen krijg je via www.encyclo.nl voor orientering en orientatie), zie je beide woorden oriëntering en oriëntatie voorkomen, maar net als op de site van de Nederlandse Taalunie, komt wel oriëntatieloop voor, maar niet oriënteringsloop. Terwijl de NOLB nu juist officieel de “Nederlandse Oriënteringsloop Bond” heet (en toch beide woorden op haar site regelmatig voorkomen, net als bij de andere verenigingen, trouwens).

De betekenis van de woorden oriëntering en oriëntatie is echter een beetje verschillend, volgens de woordenboeken:

oriëntering is het draaien of richten van iets, een rotatie uitvoeren (bijvoorbeeld het oriënteren van de kaart mbv. een kompas tov. het landschap); het zich-oriënteren; dus het doen
oriëntatie is het vermogen tot plaatsbepaling ten opzichte van de omgeving; de plaatsbepaling; het georiënteerd zijn

Maar heel duidelijk is het onderscheid niet. Beide woorden kunnen op zowel de relatieve plaatsbepaling, als de relatieve richting slaan. Zou het verschil dan zitten in de betekenis uitgang van het woord? Andere woorden die een vergelijkbare -tatie/-tering variant kennen zijn:

argumentatie/argumentering
facilitatie/facilitering
fragmentatie/fragmentering
implementatie/implementering
interpretatie/interpretering
limitatie/limitering
reglementatie/reglementering

Echter, deze hebben allemaal in beide gevallen dezelfde betekenis, waarbij moet worden opgemerkt dat de -tatie variant verreweg het meeste voorkomt. Een paar woorden hebben echter een verschillende betekenis afhankelijk van de uitgang:

In meer of mindere mate kan je hier, net als in orientatie/orientering, een zijn en een doen in zien. Maar het blijft een grijs gebied. Het helpt dus niet erg om naar andere woord-uitgangen te kijken.

Als je het zo leest doen we aan oriëntering, we bepalen onze plaats, en onderweg doen we af en toe aan oriëntering van de kaart of ons zelf. Dat laatste dan bij de minder bedrevenen (waaronder ik zelf) veelal stilstaand, waardoor oriënteringslopen dan even wat minder voorkomt (maar daar wordt aan gewerkt).

Het doel is daarentegen wel de oriëntatie van onszelf. Als je het goed doet ben je niet aan het oriënteren, maar houd je de oriëntatie van start tot de finish vast. En gaat het behalve om kunnen hardlopen ook om het vermogen tot plaatsbepaling: oriëntatie.

Oriëntatie is meer de essentie van de sport dan oriëntering.

Pragmatisch kan je stellen dat het er om gaat dat men weet wat er bedoeld wordt. En ik denk, net als Alfred op het forum, dat het Nederlandse oriënt/erings/atie/lopen al een stuk eenduidiger is dan het Engelse orienteering (zonder lopen). Dus waar hebben we het over? We mogen toch zelf bepalen hoe het heet wat we doen?

Het moois is nog Walters observatie:

Op Vlaams niveau (VVO) spreken we over “Vlaams Verbond voor Oriënteringssporten” terwijl dit op het nationale niveau (BVOS) “Belgisch Verbond voor Oriëntatiesporten” is.

In België hebben ze dus gewoon officieel de keus! Of promoveer je van oriëntatie- naar oriënteringsloper zodra je op nationaal niveau gaat presteren? Is oriëntering die zwarte band onder de oriëntatie?

Ten slotte kan je je afvragen wat wij als lopers nou eigenlijk zijn: Oriënteerders, Oriëntatielopers, Oriënteringslopers of Oriënteurs? Ik houd het bij Oriënteurs. Gewoon, omdat ik dat een mooi woord vind. En omdat het korter is dan hic-qui-scit-accedere-ad-propositum.

Stress op de Oostappense Heide

13/05/2012Overpeinzingen, Verbeterpuntjes, Verhaal, WedstrijdJan-Gerard

Gejeremiëer

Het heeft even geduurd voordat ik mijn blogje over de laatste loop op de Oostappense Heide had bijgewerkt, maar dat heeft een reden. En die is onderdeel van het verhaal. Was ik meteen gaan typen, dan was het een klaagzang geworden.

Want het ging niet lekker, dacht ik. Tot ik de Splits zag, en opviel dat ik de eerste helft tussen plaats afwisselend tussen plaats 3 en 6 liep. Helemaal niet verkeerd, bij 24 lopers!

De Splits waren echter nog niet meteen beschikbaar, zodat ik twee dagen in mineur was. Door een last-minute update van omloop 1 waren de Ocad file, de Helga file, de postomschrijving, de kaart, en de gelopen route niet meer helemaal het zelfde. En dan raakt de PC van de wap, zodat de online-uitslagen van omloop 1 niet meer werkten. Wat wel werkt is de gecorrigeerde Splitsbrowser file op mijn eigen servertje; en daar werd ik weer blij van. Nou ja, ten dele.

Wat niet werkte was mijn hoofd. In de 2e helft van de koers. Twee aanleidingen, één redenen:

Ik raakte in de war omdat de postnummers in ‘t veld niet klopten met de postomschrijving. En ging tot twee keer terug (zie ook het wedstrijdverslag). Gebrek aan concentratie was het gevolg.
Ik onderschatte de posten die ik de dag er voor zelf had uitgezet, en liep juist dáár verkeerd. Terwijl ik daar het gevoel had dat ik het juist goed moest doen. Frustratie en onzekerheid volgden.

Stress

En de reden dat het niet lekker liep was toen stress. Een effect waar je wel vaker over leest, en de reden waarom je altijd moet zorgen dat je gegarandeerd de 1e post probleemloos vindt (lees Luc Cloostermans). Maar de 9e en 19e zijn dus ook cruciaal, zo blijkt.

Stress? Ja, een gevoel dat ik haast heb. Tijd gebrek. Klinkt triviaal, in een wedstrijd, en ook is een dosis spanning essentieel. Maar niet als dat tot een te sterk gevoel leidt dat je iets hebt goed te maken, te compenseren. Door bijvoorbeeld stukjes af te snijden.

Afsnijden om het afsnijden, niet omdat het sneller is.

Juist omdat je dat toch al moet doen, als het sneller is ten minste, in een O-loop, kan je alleen maar meer afsnijden als dat extra risico inhoudt. Of je gaat afsnijden om het afsnijden, niet omdat het sneller is. En niet op de kaart kijken, omdat je gokt “dat het wel klopt”, en niet-kijken ietwat tijd scheelt. Of kaartcontact verliezen, omdat je denkt straks wel weer te herkennen waar je bent. En dat alles omdat je tijd in wilt halen. Of er althans een piepklein kansje is dat het tijd scheelt.

Niet doen, dus! Niet in de stress schieten. En zorgen dat, als dat gebeurt -en dat zal toch wel, want dat verander je niet zo maar-, je er wijs mee omgaat. Dus ondanks de spanning, tijd blijven nemen voor dingen die je anders ook zou doen. Je kan niet inlopen door de juiste route te verwaarlozen. Hooguit door harder te rennen waar dat kan (wat dan weer zuurstof en dus scherpte kost – dus het kan ook tegen je werken). En misschien door verstandige risico’s te nemen. Maar daarin zit hem juist de crux: schat je de risico’s wel goed in als je gestressed bent?

Ik denk het niet. Ik denk dat ik, onder druk, juist even voor rust moet kiezen, niet door langzamer te gaan, maar door op zeker te spelen. Die verloren tijd is jammer, maar loop ik niet meer in. Als ik er niet nog meer tijd door verlies is dat de grootste winst. En het is vaak al twijfelachtig of doorsteken tijd oplevert; dan kan ik beter even flink doorlopen op het pad, en zo een gegarandeerd aanvalspunt voor de volgende post benutten.

Tot zo ver de verbeterpuntjes van deze loop. Hoe ging het in het veld?

De wedstrijd

Het eenvoudigst is gewoon deze Headcam video te bekijken. Want ik heb weer met een camera op mijn hoofd gelopen. En dit is het resultaat van een Contour Roam, een Garmin Foretrex 305, Quickroute, RGMapVideo, en een halve dag rekentijd. Oordeel zelf.

Leg 1 ging er meteen fel tegenaan: 4’22″/km. En leg 2, dwars overal doorheen, was met 5’34″/km ook niet slecht. Leg 3 liep ik wat te ver, vreemd genoeg, nadat ik er aanvankelijk recht op af was gelopen. Leg 5 en 6 verdeed ik wat tijd met kaartlezen.

En bij leg 7 had ik veel beter het pad kunnen nemen, maar, ietwat overmoedig, ging ik door het veld met 1 meter hoog gras. Op het been naar 8 liep ik eerst achter Frank Buytaert, denk ik, aan, maar dat hiel ik toch niet vol. Daarna kwam het lange been naar 9, dat met 5’45″/km nog best rap ging, maar met 34.1% extra afgelegde afstand ten opzichte van de rechte lijn, was het geen geweldige prestatie; het was ook de 16e tijd in de splits. Hier begon ik toch al wat stomme dingen te doen, en hield geen goed kaartcontact. Ik meende al te weten waar de post stond, en dat ging dus fout.

Vanaf dat moment gingen dingen minder goed. Naar 10 viel nog mee, maar naar 11 toe kon ik de post niet goed vinden, en ging te vroeg al vertragen. Beter had ik het pad en de weg kunnen volgen. Legs 12 en 13 waren op zich goed, en ook redelijk snel, maar bij post 13 raakte ik in verwarring. Het post-nummer klopte niet, en ik heb bijna een minuut stilgestaan, speurend naar een andere heuvel met vlag, en kijkend op de kaart mijn positie toch echt wel klopte. Tot andere lopers aankwamen, en opmerkten dat er een post ontbrak in de nummering en alles 1 regel wat opgeschoven. Die laatste opmerking bleef bij mij niet hangen.

Legs 14 t/m 17 gingen weer aardig, maar post 18 had ik de dag tevoren weer zelf neergezet, en dus kon ik hem niet meer vinden. Zou ik hem te goed verstopt hebben? Ik denk dat ik hem gewoon heb onderschat. Leg 19 ging het fout. Een groot aantal lopers liep zo’n beetje samen van 18 naar 19, wat voor extra snelheid zorgde, maar ik ontdekte bij 19 opnieuw dat de nummering niet klopte. In plaats van in te zien dat dat voor alle laatste posten gold, ging ik er van uit dat de anderen het fout hadden, ik me mee had laten nemen naar de verkeerde post, en mijn post 19 elders stond. Zou dit dan al 20 zijn?

Pas na 5 minuten zoeken en dwalen was ik er zeker van dat deze 19 toch de juiste was. Maar toen was de vaart er al uit. Met 8’51″/km naar 20. En ook de route naar 21 was belabberd. Ik verloor kaartcontact, vertelde me bij het bijhouden van de paden die ik was gekruisd, telde geen passen meer, en concludeerde voortijdig dat ik door het donkergroene bos liep, terwijl het het groen-gearceerde perceel was. Waardoor ik na een doorsteek bij 22 belandde, in plaats van 21. De nummering was wel weer juist, maar dit was toch niet de bedoeling. Dus herorienteren, en op weg naar de echte 21. De 22 terugvinden was daarna eenvoudig, op een stuk prikkeldraad na.

Met wat goed te maken, ging ik op tempo 4’58” op weg naar post 23. Dat kostte me echter zoveel extra zuurstof en hartslag, dat m’n routekeuze naar 24 op zijn zachtst gezegd belabberd was. En naar 26 raakte ik van slag van iemand die nogal opgewonden stond te roepen dat de post verkeerd stond, waardoor ik ook ging zoeken. Hij stond gewoon 30 meter verderop, net als op de kaart. Het eindsprintje over de laatste 70 meter naar de finish kon niet veel meer goed maken.

Maar als ik uit de leermomenten mijn conclusies trek, en hier de volgende keer ook wat mee doe, was het een zeer productieve race.

Confronterend nadeel van een camera op je hoofd…

13/04/2012Materiaal, Overpeinzingen, VerhaalJan-Gerard

Dat is natuurlijk pijnlijk: zien dat je iets wel gezien hebt maar niet gekeken (als in: gehoord maar niet geluisterd). Het is me overkomen. Ik wist niet wat ik zag toen ik laatst mijn headcam video van 19 januari, op de kaart Pijnven noord, aan het bekijken was. Ik herinner me dat ik daar bij post 2 hopeloos lang heb lopen zoeken. Ik was niet verdwaald, ik wist precies waar ik was, maar ik zag de wit-oranje postzak niet. En dan ga je zoeken, want misschien staat hij verkeerd. Of zit ik er zelf net naast. Wel een minuut of 3:20 heb ik rondjes gelopen. Je kan het op de kaart goed zien: Quickroute. Ik kwam van uit het oosten aanlopen, sneed een stukje af, en zo te zien, vlak voordat ik bij de post was, draaide ik naar links. Om dan te gaan rondfladderen. En uiteindelijk, nadat vanuit de tegenovergestelde richting naar de post was gelopen, zag ik de vlag. Tot zo ver het acceptabele stuk van het verhaal.

Maar kijk nu eens naar het onderstaande fragment:

Ik loop op de post af, in mijn ooghoek is hij even zichtbaar, rechts in beeld, wanneer het filmpje even stop, en ik loop er stomweg voorbij! Wat een blunder! Een beetje Sven Kramer die op de Olympische Spelen van 2010 de verkeerde baan nam. Alleen dan zonder coach die ik de schuld kan geven.En weer was het de camera die het pijnlijk hard vastlegde.

Dus nu dient de vraag zich aan: film ik de volgende keer weer, of laat ik het hier bij? Nou ja, de rest maakt het toch wel de moeite waard om terug te kijken.

Bloggen in Nederlands of Engels, that’s the question…

22/03/2012English, Overpeinzingen, WebsiteJan-Gerard

Ik vraag me af of ik deze blog niet in het Engels moet schrijven. I wonder whether I should write this blog in English or in Dutch. Orienteering is an international sport, and the North is everywhere (roughly) the same. Orienteering is een internationale sport, mijn publiek is uiteraard groter als ik in het Engels schrijf. I have a bigger audience when I writing in English. Aan de andere kant, het leest voor Nederlanders en Belgen wel weer lekkerder als ik het in het Nederlands houd. On the other hand, for the Swedish, it would be better if I would not write in Swedish, since that wouldn’t be readable at all (given my Ikea-only vocabulary). De vraag is dus: wie is mijn publiek or who is my audience?

Wie is mijn publiek?

En omdat ik ook een deel voor mezelf schrijf, gewoon om mijn gedachten op papier te zetten, denk ik dat ik het bij Nederlands houd. However, the bigger the audience, the bigger the motivation to write.
Mee eens? Of niet? Laat dan een berichtje achter onderaan deze pagina. Want ik wil best voortaan Engels typen.
De Google Ads heb ik weer van mijn site gegooid: niemand klikte ze aan, en het werd er niet overzichtelijker op. Leuk om eens te proberen, maar je moet wel heel veel bezoekers trekken wil dat wat opleveren. Wel kreeg ik meer hits om mijn blog-site zo lang ik Google betaalde (50 euro gratis introductie krediet) voor het plaatsen van links op andere sites.

Orienteering is menselijk…

14/01/2012OverpeinzingenJan-Gerard

Kijk maar naar dit filmpje over Olifantenpaadjes. Of deze link. En toch, als je kijkt hoe de paadjes vaak een beetje rond lopen, valt er nog wat te verbeteren. Pas als de paadjes voldoen aan deze eigenschappen, waaronder de Wet van Snell, is er spraken van optimale O-lifantenpaadjes.

Wijzen is onbeleefd

30/10/2011OverpeinzingenGC33W5KJan-Gerard

“Waar?” “Daar!”, en zij wees in de richting van het zuiden.
“Hoe ver?” “Twee uur gaans.” En hij ging op pad, met zijn gezicht naar de zon. Na precies twee uur zette hij zijn rugzakje neer, pakte er een appel uit, beet er een flinke hap uit, en ging op zoek.
Na ruim een uur gaf hij het op, pakte zijn rugzak weer op, hing hem over zijn schouders, en liep terug. Weer twee uur later kwam hij bij het bankje aan waar zij nog steeds op zat. “Die speld ben je kwijt. Ik zou maar een nieuwe gaan kopen.” En zonder verder wat te zeggen, liep hij terug naar zijn hooiberg.

Beetje sneu natuurlijk, maar je snapt wel waar het aan lag; “twee uur gaans” is natuurlijk wat vaag, en een beetje wijzen naar het zuiden, wat op zich een exacte richting is met onze huidige kennis, klinkt niet echt als een richtingsbepaling met meerdere decimalen.
Nee, we hebben tegenwoordig moderne middelen. Op korte afstanden voldoen een peilkompas en passen tellen (hoewel dat laatste natuurlijk ook in de tijd van de Neanderthalers werkte; maar ze wisten nog niet wat een meter was), en op de langere hebben we bijvoorbeeld GPS-en die een absolute plaatsbepaling leveren.

Wijzen

En zo zou je kunnen zeggen dat wijzen onbeleefd is, net als mensen met een kluitje het riet in sturen, van het kastje naar de muur, en het bos in zonder kompas of GPS en goede aanwijzingen en kaarten. Toch is wijzen heel handig, en dikwijls de beste optie. Wil je weten hoe je naar het station loopt? Je wordt niet blij als die behulpzame dame op straat je een coördinaat geeft, met wat letters en nog meer cijfers: 31 U 670765 5702726. “Daar heen, vijf minuutjes lopen” wil je horen!

Iets moeilijker wordt het als je een vlaggetje of doosje moet vinden, dat een eind verderop ligt, en niet zo makkelijk herkenbaar is als een station, van 300 meter afstand. Laten we het concreter maken: je wilt vanuit N 51° 25.854 E 005° 29.263 precies 1013 meter lopen, onder een hoek van 47° met het noorden. Dan kan het nog mis gaan omdat ik niet zei of je het noorden links of rechts of laat liggen, maar ik had N 51° 26.227 E 005° 29.902 voor ogen. Twee opties: je weet waar je bent (hoop je), op de kaart, en je hebt een gradenboog en schaalverdeling, zodat je kan uitpeilen op papier waar je doel ligt, er even van uit gaande dat je dat vervolgens ook in het echt kan vinden, of je hebt een goed kompas en een absolute stapgrootte, en je loopt er zo ongeveer als hier, in een rechte lijn naartoe. O, ja, je kan ook nog een projectie maken op je GPS, als je die hebt.

Als jet het goed doet, zit je er hooguit 8.85 [m] naast, want dat is de halve afstand tussen twee graden, op die 1013 meter afstand. Niet helemaal niks. Had ik 47,0° gezegd, dan wist je het nog zekerder: op minder dan een meter nauwkeurig. Of niet, want hoe nauwkeurig kan je precies 47 graden uitpeilen, of hoe lang kan je precies met de naald van je kompas op het streepje 313 lopen? En klopt mijn 47 wel, want die heb ik ook maar ooit, wellicht met dezelfde middelen, opgemeten.

Over dit soort dingen gaat dit artikeltje ongeveer. Lees verder!

Koersen

Ik moet altijd even nadenken, wat het verschil is tussen de Engelse termen bearing, course, en heading, en ook tussen het Nederlandse peiling en koers; een mooi woord voor heading kennen we niet, of het moets “voorliggende koers” zijn. Dus herhaal ik het hier even, dan onthoud ik het zelf vast beter.

Een peiling is de richting naar een punt. Op ieder moment. Op het kompas is het de richting van het punt waar je heen wilt, afgelezen als de nul van de kompasroos naar het noorden wijst. Dus als een punt zich pas oostelijk van je bevindt loopt de lijn naar dat punt vanuit het midden van de roos over de “90” heen. Als je dat punt peilt lees je 90° af: de peiling, of eng.:bearing. Loop je een stukje naar het noorden, dan verschuift de peiling naar een groter hoek (in dit voorbeeld).

De koers (eng.:course) is de lijn die je wilt volgen om ergens te komen. Dat lijkt het zelfde, maar de koers verandert in eerste instantie niet als je beweegt, en afwijkt van de koers. De peiling naar je doel verandert, en je “ligt niet meer op koers”, maar de koers blijft onveranderd. Tot je besluit en nieuwe koers te varen, lopen, vliegen, om bij het doel te komen. Dat mag, maar dat doe je niet meteen, want dikwijls is die koers niet voor niets gekozen. Als je een lijn op de kaart tekent, of denkt, is dat de koers. En die hoeft niet altijd direct naar het doel te lopen, bijvoorbeeld omdat daar een berg, een meertje of een eiland tussen ligt. Kortom, vaak is de koers slim gekozen, en niet de kortste, maar wel de snelste weg naar het doel. Met andere woorden, vaak wil je terug naar de koers als je er van afwijkt, en verleg je niet meteen zomaar de koers. Was je vanaf het begin af aan op koers gebleven, dan was de koers wat het kompas al die tijd aan had gewezen.

Tenslotte het Engelse heading (mocht je een mooie Nederlandse term hier voor kennen, onder aan deze pagina is ruimte voor commentaar): eigenlijk is dat waar je neus heen wijst, of je een boot, een vliegtuig, of een loper bent. Heeft dus niets met koers en peiling te maken, maar als je vooruit gaat, en een doel voor ogen hebt, komen ze vaak toch wel in de buurt. Het is de kompasrichting die overeenkomt met je eigen voorkant. Echter, niet altijd ga je ook die kant uit. Een vliegtuig met zijwind, een boot die verlijert, een loper met een scheve neus, allemaal gaan ze een ander kant uit dan waar hun neus heen wijst. Geen probleem als je weet wat de afwijking is.

Duidelijk?

Kompas

Ik heb al een paar keer “kompas” gezegd. Handig ding. In essentie is het een apparaatje met een wijzer, een pijl, een naald, die gemagnetiseerd is, en waarvan de magnetische zuidpool van een markering, een pijl of een kleur, is voorzien, die naar de Noordpool wijst, mits deze naald vrij kan draaien. Van alles wordt toegevoegd, vloeistof, spiegels, lenzen, om het kompas nog bruikbaarder te maken, maar de magnetische naald is essentieel. Doorgaans is er nog een roos, met een graden-verdeling die meedraait met de naald, of een schaalverdeling die stilstaat, waar de naald een waarde op aanwijst. Zo kan je ook nauwkeurig in andere richtingen dan het noorden of het zuiden gaan.

Meer…

Op dit moment ben ik even uitgeschreven. Maar er komt meer.

Waarom π en niet τ

11/07/2011OverpeinzingenGC33W5K, geocache, geocaching, korste route, pi, rekenen, sinterklaas, wiskundeJan-Gerard

Tijdens een rondje hardlopen schieten soms de vreemdste dingen te binnen. Dan ga ik ineens lopen rekenen, en kom tot de conclusie dat π zo gek nog niet is: τ hebben we in elk geval niet nodig, zoals in dit filmpje wordt gesuggereerd:

Ik liep een stuk (een forse taartpunt) tegen de klok in langs de Eindhovense ring, en bevond me in de buitenbocht. Ik kwam immers van buiten de ring, en was nog voor het oversteken rechtsaf geslagen, zodat ik op de ventweg linksom liep. De buitenbocht is om, dat weten we allemaal. Maar ja, het is wel een hele flauwe bocht, dus wat maakt het uit?
Ringwegeindhoven
Ik volgde een tijdje de ring, sloeg toen af met het centrum in mijn rug, om later weer terug te keren op de ring. Dit maal liep ik met de klok mee, want ik ging weer richting huis.

Op een gegeven moment passeerde ik een tunnel, en besloot onder de ring door te gaan, om verder over de binnenbocht te lopen: veel korter, toch? Maar ja, al die tijd dat ik onder dat tunneltje door liep (of anderszins overstak van buiten naar binnen naar buiten in de bocht) was ik geen meter verder de ring rond gekomen.

Zo kwam het dat ik me afvroeg: hoeveel kilometer moet je over een rondweg lopen, wil het de moeite zijn om de binnenbocht te nemen? (Vooropgesteld dat je aan de buitenkant begint.)
Stel je voor: je gaat in de buitenbocht staan, loopt naar de binnenbocht, en direct weer terug naar de buitenbocht -omdat je helemaal niet de rondweg wilde volgen-. Dan is het overduidelijk dat het niet loont. Loop je echter het hele rondje, of twee, of oneindig veel keer, dan is het zeker wel de moeite van het oversteken waard. De waarheid ligt ergens in het midden. Maar waar?

Ik herinnerde me een vraagstuk van de middelbare school, waarop afgaande ik mijn vraag eigenlijk wat anders moest verwoorden: Stel, ik heb een touwtje rond de wereld gespannen, en dat wil ik een meter optillen. Dan moet ik het touwtje wel wat langer maken (gegeven dat het niet uit kan rekken). Maar als ik een touwtje rond een bal span, en de lus een meter ruimer maak -dus met overal een meter tussen bal en touwtje-, moet ik dan het touwtje meer of minder langer maken dan het touwtje rond onze aardbol?

Het antwoord is: geen van beide. Evenveel dus. 6,282 meter -en een beetje- om precies te zijn. Het klinkt ongelooflijk, dat een lus rond de hele aarde maar een ruime 6 meter langer hoeft te worden om 1 meter boven het aardoppervlak te zweven, en dat het niet uitmaakt of die planeet een straal van ruim 6300 kilometer heeft, of 15 centimeter, maar het is waar.

De lengte l van een cirkel met een straal r (de straal van de aarde of van de bal) is $l = 2 \cdot \pi \cdot r$ . Als ik het touwtje overal een meter boven het aardoppervlak houd wordt de lengte $l_\textnormal{\'{e}\'{e}n meter boven de aarde} = 2 \pi(r_\textnormal{aarde} + 1 [m])$ , en als ik de lus een meter om de bal leg wordt zijn lengte $l_\textnormal{\'{e}\'{e}n meter rond de bal} = 2 \pi (r_\textnormal{bal} + 1 [m])$ .

Maar dat kan ik weer schrijven als $l_\textnormal{\'{e}\'{e}n meter rond de bal} = 2\pi r_\textnormal{bal} + 2\pi\cdot 1[m] = l_\textnormal{strak om de bal}+2\pi[m]$ . En dus heb ik $2 \pi [m]$ extra touw nodig voor de bal, maar omdat $l_\textnormal{\'{e}\'{e}n meter boven de aarde} = 2\pi r_\textnormal{aarde} + 2\pi\cdot 1[m] = l_\textnormal{strak om de aarde}+2\pi[m]$ geld dat ook voor de aarde.

Het maakt dus, volgens dezelfde redenering, niet uit of ik de rondweg rond een grote stad rond loop, of rond een kleine, maar het gaat om de hoek van de cirkelboog die ik volg. En dat is leuk, want dat betekent dat ik een vuistregel kan opstellen voor de beslissing of ik de ringweg oversteek of niet, afhankelijk van de grootte van de taartpunt (of het aantal graden dat ik de ringweg volg).

Hoeveel graden moet je over een rondweg lopen, wil het de moeite zijn om -buiten beginnend- de binnenbocht te nemen?

Maar dan is er nog iets: als ik nou een hele brede ringweg heb, met 6 banen heen en 6 banen terug, dan loont het natuurlijk veel meer de moeite om de binnenbocht te pakken, dan wanneer het een zandpad is. -Zou je denken.- Maar tegelijkertijd ben ik ook meer tijd, en meters, kwijt om van buiten naar binnen en binnen naar buiten te lopen, wat me weer geen hoek-voordeel oplevert bij mijn rondgang. Met andere woorden, ik maak wel meters, maar geen graden, en we hadden net vast gesteld dat het om dat laatste ging.

Weet je wat? We gaan het gewoon uitrekenen! De vraag wordt nu: hoeveel graden moet je ronde een punt lopen, wil het de moeite zijn om de binnenbocht te nemen?

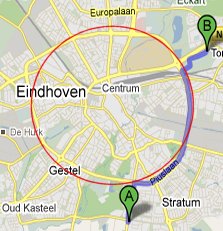
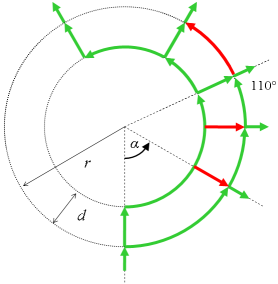Laat de breedte van de rondweg d [meter] zijn, en de straal r. En je loopt vanaf 0° tot aan hoek α. Voor de berekening gebruiken we even $\beta=2\pi\cdot\alpha/360^{\circ}$ , dus de hoek $\beta$ in radialen. De weg die je aflegt is dan $l_\textnormal{via de binnenbocht} = d+(r-d)\beta+d$ via de binnenbocht, en $l_\textnormal{via de buitenbocht} = r\beta$ . Het loont dan dus als $l_\textnormal{via de binnenbocht}<l_\textnormal{via de buitenbocht}$ , oftewel, als $d+(r-d)\beta+d<r\beta$ . Dat laat zich vereenvoudigen tot $2d+r\beta-d\beta<r\beta \Leftrightarrow 2d-d\beta<0$ , en dus $2d<\beta d \Leftrightarrow \beta>2$ . Met andere woorden, als ik meer dan $\alpha=\beta\frac{360^{\circ}}{2\pi}=360^{\circ}/\pi$ rond ga, kan ik beter oversteken. Dat is dus bijna 115° (114,5915590261647…)! Best veel als je het zo bekijkt. Bijna vier uur op de klok.

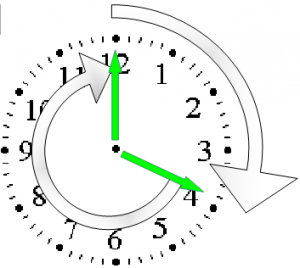Onthoud dat goed: moet je meer dan één Pi-de deel van een taartpunt (een pie) rond een punt, neem dan voortaan de binnenbocht. En anders, ook al lijkt het om, kan je beter in de buitenbocht blijven.

Het maakt niet uit hoe groot de cirkels zijn, zowel de binnenbocht, als de buitenbocht niet. 115° is 115°. Maar ik ben er wel van uit gegaan dat je alleen dwars (radieel) over kunt steken, dus niet spiraalvormig van buiten naar binnen en van binnen naar buiten of anderszins schuin, maar alleen in rechte lijnen van en naar het centrum.

Grappig vind ik het wel dat het antwoord niet $\frac{1}{3}$ e is of zo, maar $\frac{1}{\pi}$ e. En dat is nou het leuke: eindelijk eens een redenering waaruit blijkt dat pi helemaal niet zo’n gek getal is. Anders had hier het $\frac{1}{2}\tau$ -de deel van een cirkel gestaan, want $\tau=2\pi$ , en dan is een $\pi$ -de toch veel mooier.

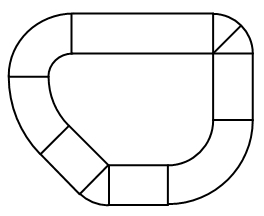Je kan je trouwens nog even af gaan lopen vragen of het uitmaakt of de betreffende rondweg rond is, ei-vormig, onregelmatig, met rechte stukken er in, maar dat hoeft niet lang te duren want hier is het antwoord: Nee! Zo lang de binnen- en buitenbocht maar overal even ver uit elkaar liggen, en de weg overal convex is, gaat bovenstaande altijd op.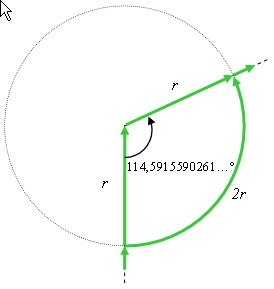

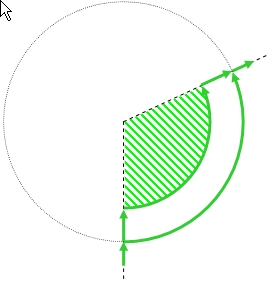Een extreem brede rondweg maakt de dingen wel eenvoudiger.

Je kan het zelfs nog eenvoudiger bekijken. Ga eens uit van een extreem brede rondweg, van de rand (straal is $r$ ) tot aan het midden van de cirkel (eigenlijk is de hele stad asfalt). Dan is de die weg $2r$ lang.
Een complete cirkel daarentegen heeft een omtrek van $2\pi r$ , en dus moet ik daar een $\frac{1}{\pi}$ ^e deel van hebben om op een cirkelboog van $2r$ uit te komen, want $\frac{2r}{2\pi r} = \frac{1}{\pi}$ .
Geldt dat dan ook voor een weg van beperkte breedte? Ja! Want als ik bij deze specifieke hoek net zo goed om kan lopen als af kan snijden, kan ik ook evengoed en “hap” ter grootte van dit cirkelsegment uit een groter cirkelsegment nemen. En de resterende vorm is weer een stukje rondweg, met een even lange binnen- als buitenbocht. Q.E.D.

JG-O

J-G's Oriënteringslopen/Orienteering site